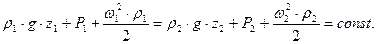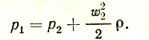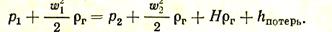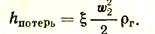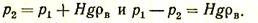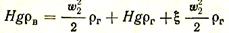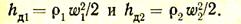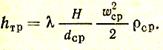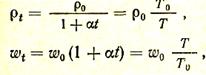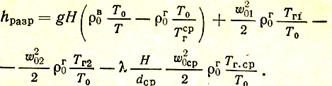Закон бернулли для печей

УРАВНЕНИЕ НЕРАЗРЫВНОСТИ. УРАВНЕНИЕ БЕРНУЛЛИ

РАЗДЕЛ 2 ОСНОВЫ МЕТАЛЛУРГИЧЕСКОЙ ТЕПЛОТЕХНИКИ

Тема 2.1 ОБЩИЕ СВЕДЕНИЯ О ПЕЧНЫХ ГАЗАХ

Печные газы – это газы, выделяющиеся при проведении металлургических процессов.

Механика газов – это наука о законах равновесия и движения газа.

Механика газов широко использует многие понятия, аналогии, уравнения механики жидкости (гидравлика, т.к. газы можно рассматривать как сжимаемые, упругие жидкости).

Для того, чтобы правильно рассчитать конструкцию печи, нужно знать законы движения и равновесия газов.

Состояние газов зависит от T, V, P.

Различают идеальные и реальные газы.

Идеальные – это совокупность молекул, лишенных сил взаимодействия.

Реальные – молекулы в газе подвержены силам взаимодействия. Эти газы обладают вязкостью, т.е. свойством оказывать сопротивление перемещению частиц.

Некоторые газы в парообразном состоянии мало отличаются от идеальных (O₂, N₂, CO и CO₂…) и к ним при обычных условиях применимы законы идеальных газов (к др. газам эти законы не применимы). 24.11.13.

Из уравнения состояния идеальных газов (Клайперона) для одного и того же количества газа следует:

= = const. (1.1)

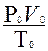
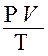
V = V₀ (1+aT) 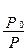, где

a = 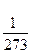– коэффициент объёмного расширения.

Вводим понятие плотности газа (ρ=кг/м 3 ) – это величина, обратная удельному объёму.

,

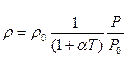
При Р =Р₀, т.е. при постоянном давлении =>

(2) ;

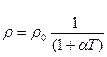
Для вакуумных печей этого делать нельзя, т.к. давление там сильно изменяется.

Вводим понятие скорости движения газов:

ω 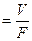(м/с), (4)

F – площадь поперечного сечения, м 2

V – расход газа в секунду, м 3 /с

При постоянном сечении канала и постоянном давлении, скорость будет изменяться от температуры, так же, как и v.

Тема 2.2 ДВИЖЕНИЕ ГАЗОВ.

II

I

Если рассмотреть участок канала переменного сечения, по которому движется газ, то по закону сохранения материи, количество газа на входе и выходе должно быть одинаково.

Q можно найти, как произведение скорости на площадь поперечного сечения и плотности в сечениях I и II.

Уравнение неразрывности потока для сжимаемой жидкости или газа.

Уравнение неразрывности потока для несжимаемой жидкости или газа.

Закон сохранения энергии на рассматриваемом участке канала может быть представлен уравнением Бернулли:

Движение газа в печи происходит под действием энергии, которой он располагает. Эта энергия может быть потенциальной и кинетической.

В механике эту энергию выражают избыточным давлением или напором, т.е. разностью между Р в каком либо сосуде и атмосферным.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Как записать уравнение бернулли для печных газов

ГЛАВА III. ОСНОВЫ ПЕЧНОЙ ТЕПЛОТЕХНИКИ

Газообразные продукты, образующиеся в процессе горения топлива, поступают в рабочее пространство печи, оставляют в нем часть своего тепла и через боров и дымовую трубу удаляются в атмосферу. В правильно сконструированной печи, во избежание подсоса воздуха, на всем протяжении рабочего пространства оттопки до пролетав боров должно быть сохранено положительное давление. Чтобы грамотно проектировать и строить печи, надо знать законы движения печных газов. Наука о движении газов называется механикой газов.

Для решения вопросов, связанных с движением газов, используется закон сохранения энергии, сформулированный итальянским ученым Д. Бернулли. Применительно к реальному газу, встречающему по пути сопротивление движению, уравнение Бернулли можно сформулировать следующим образом: при установившемся движении реального газа для каждой частицы сохраняется неизменной сумма напоров статического, геометрического, динамического и напора, потерянного на сопротивления (йпот). При движении газов происходит превращение напоров: геометрического в статический, статического в динамический, динамического в статический или потерянный.

Применение уравнения Бернулли

Трудно назвать раздел механики газов, где не исполь­зовалось бы в той или иной мере уравнение Бернулли. По­знакомимся лишь с некоторыми наиболее важными случа­ями применения этого уравнения.

Истечение газов через отверстия и насадки

Истечение газов через отверстия и насадки наблюдает­ся при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истече­ние. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.

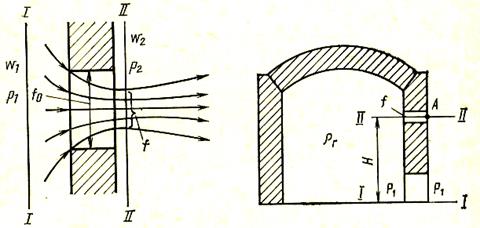
Отверстия с острыми краями. Положим, что из сосуда очень больших размеров, давление в котором р₁, газ выте­кает через отверстие сечением f₀ в среду с давлением р₂. Для определения скорости истечения газа w₂ напишем уравнение Бернулли для сечений I и II (рис. 9). Поскольку температура газа неизменна, постольку h_г1 = h_г2. В этом случае, пренебрегая потерями, можно написать

(21)

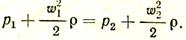
Вследствие большого размера сосуда можно принять w₁= 0

(22)

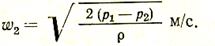
В силу инерции частичек истекающего газа сечение струи f меньше сечения отверстия f₀. Отношение f/f₀= e называется коэффициентом сжатия струи. Скорость w₂ фактически относится не ко всему сечению отверстия f₀, а лишь к сечению струи f. Для определения расхода газа че­рез отверстие f₀ найдем V = w₂f. Но f = ef₀ следовательно,

(23)

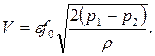
С учетом гидродинамических потерь при истечении че­рез отверстие выражение (23) принимает вид (м 3 /с)

(24)

Рис. 9. Истечение газа из отвер- Рис. 10. Истечение из отверстия в

стия в тонкой стенке стечке печи

Смысл коэффициентов j и m, ясен из следующего при­мера.

Истечение из отверстия в стенке печи (рис. 10) — весь­ма распространенный на практике случай. Рассмотрим подобный случай истечения (с учетом потерь) из отверстия сечением f, расположенного на высоте Н от уровня пода печи. Напишем уравнение Бернулли для сечения I и точки А в сечении II:

Скорость движения газов в отверстии w₂много больше скорости w₁; исходя из w₂ññ w₁, принимаем w₁ = 0.

Как следует из изложенного выше, потери на местные сопротивления могут быть определены как

Так как печь сообщается с атмосферой на уровне пода, то статическое давление газа внутри печи и давление воз­духа снаружи равны между собой и равны р₁.

Давление р₂ в точке А соответствует атмосферному дав­лению на высоте H от уровня сечения I, т. е.

С использованием этих зависимостей уравнение Бернул­ли принимает вид

(25)

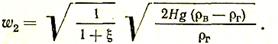
Величина 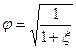учитывает гидравлическое сопро­тивление отверстия, через которое происходит истечение.

Количество истекающей из рассматриваемого отвер­стия среды (м 3 /с) V = w₂f₂, где f₂ — сечение струи, м 2 .

Но если использовать понятие коэффициента сжатия струи e = f₂/f, то

.

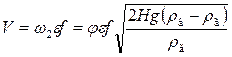
Произведение je = m называют коэффициентом расхода.

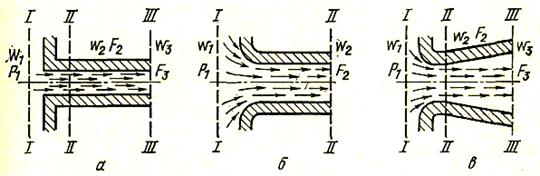
Истечение через насадки. Насадком называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадка обычно составляет 3—4 его диаметра. Ко­личество газа, протекающее через насадок, при прочих равных условиях зависит от формы входных кромок и формы самого насадка. Рассмотрим насадки трех видов, представленные на рис. 11. Пользуясь уравнением (22), получим для них следующие расчетные формулы: для насадки с открытыми кромками

(26)

(27)

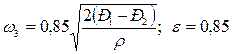
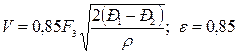
Для насадков с закругленными кромками и диффузора

(28)

Рис. 11. Истечение газа через цилиндрические насадки:

а — с открытыми кромками; б — с закругленными краями; в — диффузор

Для этих насадков в сечении ІІІ сечения струи и отвер­стия равны друг другу и поэтому здесь e = 1,0. Сравнение выражений (26), (27) и (28) показывает, что наибольший расход при одинаковом значении р₁ — р₂и при одинаковом минимальном сечении насадков получается при истечении газа через диффузор, так как площадь выходного сечения у диффузора F₃больше, чем у насадков других типов. Угол конусности диффузора не должен превышать 6—7° во избежание отрыва потока от стенок диффузора.

Истечение газов через небольшие отверстия в стенках печи (например, гляделки) можно рассчитывать по фор­мулам для цилиндрического насадка.

Дымовая труба. Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение соз­дается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному, как будет показано ниже, разностью плотностей холодного наружного воздуха и горячих газов. Найдем зависимость разреже­ния, создаваемого трубой, от высо­ты трубы Н и температуры газов. На рис. 12 представлена схема ды­мовой трубы. За уровень отсчета принимаем сечение ІІ. Напишем уравнение Бернулли в избыточных давлениях для сечений І и ІІ:

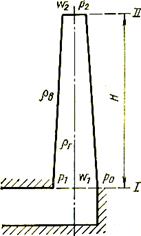
Труба в сечении II сообщается с атмосферой, поэтому h_ст2 = 0. Из приведенного выше уравнения сле­дует, что статическое давление в основании трубы

h_ст1 = – h_г1 + h_д2 – h_д1 + h_пот.

Ввиду незначительных скоростей движения газов в тру­бе величины потерь, выражаемые в правой части приведен­ного выше уравнения тремя последними членами, значи­тельно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, статическое давление в основании трубы будет отрицательным, т. е. там будет разрежение. Умножив правую и левую части последнего уравнения на минус единицу, получаем

Потери давления в трубе h_пот складываются из потерь на трение h_тр и потерь, возникающих при выходе газов из трубы в атмосферу и равных xh_д2. Учитывая, что коэффи­циент местного сопротивления на выходе из трубы ра­вен единице (x = 1), можно написать, что

Вследствие этого уравнению (29) можно придать сле­дующий вид:

Для того чтобы получить окончательное выражение для h_разр, в уравнение (29) необходимо подставить все входя­щие в него величины. Температура газов по высоте дымо­вой трубы и ее сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения га­зов в дымовой трубе определяются по средней температу­ре по высоте трубы. Величина геометрического давления h_г, входящего в уравнение (29), выражается уравнением (13). Динамические давления будут соответственно равны

Потери давления на трение находят по уравнению

Подставив в уравнение (29′) значения h_г, h_д1, h_д2, h_тр и выразив их через скорости и плотности при нормальных условиях (w₀ и r₀) по указанным выше выражениям, окон­чательно получаем (Па)

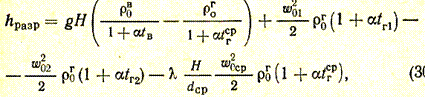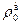
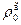
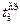
где h_разр — действительное разрежение в основании дымо­вой трубы (сечение I), Па; и — плотность соответст­венно воздуха и газов при нормальных условиях, кг/м 3 ; d_ср — средний по высоте диаметр трубы, м; w₀₁ и w₀₂ — скорость газов в сечениях I (в основании трубы) и II (в устье трубы) при 0°С, м/с; w_0ср — средняя скорость га­зов по высоте трубы при 0°С, м/с; t_в — температура окружающего воздуха, °С; — средняя температура газов по высоте трубы, °С; t_г1 и t_г2 — температура газов в сечениях I и II, °С.

где Т₀ = 273 К,то выражение (30) может быть переписано следующим образом:

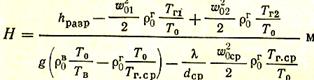В расчетах разрежение в основании дымовой трубы принимают обычно с запасом, равным h_разр = 1,3S h_пот. Ве­личина S h_пот представляет собой суммарные потери напо­ра на пути движения газов от печи до основания дымовой трубы.

При расчете дымовой трубы внутренний диаметр в устье ее d_у(на выходе) принимают, исходя из скорости газов, равной 3—10 м/с (при скорости выхода газов, не меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы d₀прини­мают в 1,5 раза больше внутреннего диаметра устья трубы d_у, т. е. d₀= 1,5d_у.

По условиям выполнения кладки d_удля кирпичных труб не должен быть меньше 0,8 м.

Падение температуры газов на 1 м высоты трубы при­нимается для кирпичных и железобетонных 1,0—1,5 °С, а для металлических 3—4°С. Ориентировочно высота тру­бы может быть определена по уравнению (30) без трех последних его членов.

Подсчитав сумму потерь всех видов на пути движения газов от печи до основания дымовой трубы, по уравнению (30′) находят расчетную высоту трубы Н. Независимо от расчета высота дымовой трубы по правилам сантехники должна быть не менее 16 м и в 2 раза выше самого высо­кого здания, находящегося в радиусе 100 м вокруг трубы.

Дата добавления: 2015-11-10 ; просмотров: 3721 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

, Основы теплотехники, Перенос энергии и массы (стр. 2 )

Из за большого объема эта статья размещена на нескольких страницах: 1 2 3 4 5

, м/с.

Умножив среднюю скорость движения газа на сечение канала , можно определить расход газа , м3/с.

Если температура газа отлична от 0оС, то плотности и скорости необходимо пересчитать на нормальные условия:

, где .

Геометрический напор нельзя измерить непосредственно, т. к. он зависит от разности плотности воздуха и газа, которую, можно вычислить, зная температуру газов.

При движении газов по полостям печей происходят постоянные превращения одного вида напора в другой. Если говорить об изотермическом течении газа, то превращения их обратимы, за исключением той части, которая теряется. На потери напора расходуется динамическое давление, которое при движении газа постоянно возобновляется за счет запаса пьезометрического давления.

Важнейшей инженерной задачей является сведение к минимуму потерь давления при движении газа. Поэтому изучение причин потерь давления является весьма важным.

2.4. Потери энергии при движении газа по трубам и каналам

Потери энергии, отнесенные к 1 кг движущегося газа, называют потерями напора; потери, отнесенные к 1м3 , называют потерями давления. Потери энергии существенно зависят от характера движения газа. Различают слоистое или ламинарное движение от турбулентного или вихреобразного. Условия существования ламинарного и турбулентного движений были установлены Рейнольдсом (1883 г.). Он доказал, что характер движения газа (жидкости) зависит от соотношения сил инерции и сил внутреннего трения в потоке. Это соотношение характеризуется некоторым безразмерным комплексом, называемым критерием Рейнольдса.

,

где – скорость движения газа, м/с;

– плотность газа (жидкости), кг/м3;

– коэффициент динамической вязкости, кг с/м2;

– коэффициент внутреннего трения при температуре газа = tг,

;

– коэффициент кинематической вязкости.

В круглых трубах поток при значениях Re 2300 течение становится турбулентным (рис. 2.6). Как видно из критерия, жидкости с большими скоростями и толщинами потока и малой вязкостью свойственно турбулентное движение, и наоборот.

.

Распределение скоростей по поперечному сечению потока, а также потери напора различны при ламинарном и турбулентном характере движения потока (рис. 2.7).

Потери напора движущегося потока

Потери динамического напора при движении потока связаны с трением его о стенки, что сопровождается переходом кинетической энергии в тепловую, и потери на преодоление местных сопротивлений.

Потери напора на трение (hтр.) определяют по формуле Жираро:

,

где – коэффициент трения, W – действительная скорость потока,– плотность потока, – длина канала, – коэффициент объемного расширения газа, – эквивалентный диаметр канала (), где F – сечение канала, S – периметр.

Для прямоугольных каналов dэкв= 2ab/a+b. Коэффициент трения – функция относительной шероховатости () и критерия Рейнольдса.

, где – средняя высота выступов (бугорков) на стенках канала.

Коэффициент трения о стенки канала

Потери напора возникают при изменении направления движения потока или вследствие изменения поперечного сечения канала (рис. 2.8). При изменении направления движения потока или сечения канала изменяются эпюры скоростей по сечению потока. Это сопровождается, также как и при трении потока о стенки канала, потерями кинетической энергии потока, необратимо переходящими в теплоту. Такие потери принято называть местными. Движение потока в прямых каналах с постоянным сечением сопровождаются только сопротивлением трению и распределены по всему каналу.

Суммарное аэродинамическое сопротивление движению газов состоит из сопротивлений трению и местных сопротивлений:

,

где К – безразмерный коэффициент местного сопротивления, определяющий долю динамического напора, необходимую для преодоления потоком того или иного местного сопротивления. Потери на изменение сечения канала следует вычислять по скорости в меньшем сечении.

Определение коэффициента местного сопротивления

Вход потока в канал с острыми кромками

К = 0.20 при закругленных кромках

Внезапное расширение канала

Постепенное расширение канала

2.5. Движение газа с низкой скоростью в каналах

Газ в рабочем пространстве печей и дымовых каналах (боровах), как правило, движется при относительно невысоких скоростях и небольших перепадах давления (до 100 Па). Изменение давления такого порядка практически не влияет на плотность газа, поэтому при расчетах печных газов обычно применяют уравнение Бернулли. Изменением плотности газа от воздействия температуры обычно пренебрегают, и расчет ведут на плотность газа при среднестатистической температуре.

Рассмотрим распределение потенциальной энергии внутри некоторого объема покоящегося газа (рис. 2.9). В этом случае его скорость и работа трения равна нулю, следовательно из уравнения Бернулли получаем:

. (3)

Пусть Н2 и Р2 будут переменной высоты и переменной давления (Н и Р), а Н1 и Р1 – их начальными значениями (Нн и Рн). Если обозначим Н – Нн = Z, то уравнение (3) примет вид . Видно, что давление газа падает с высотой. Температура газа в печи выше, чем температура окружающего воздуха, и следовательно плотность воздуха больше плотности газа. Как будет распределяться избыточное давление на стенки сосуда, заполненного газом, более легким, чем окружающий воздух?

Нижняя часть сосуда сообщается с воздухом. В плоскости раздела давление одинаково. Выше уровня Нн давление газа и воздуха падает в соответствии с уравнениями:

,

.

Вычитая, получим , т. к. плотность воздуха выше плотности газа, то давление горячего газа в сосуде (печи) всегда выше, чем давление окружающей атмосферы. Если рабочие окна печи находятся в районе пода, то давление приблизительно равно атмосферному. Избыточное давление внутри рабочего пространства печи возрастает от нуля до максимума под сводом.

Истечение газа через отверстия

Цель расчета истечения – найти скорость и расход газа, выходящего из отверстия (рис. 2.10). При низких скоростях истечения (150–200 м/с) газ можно считать несжимаемой жидкостью. Пусть газ вытекает из емкости больших размеров по сравнению с размерами отверстия, тогда можно принять скорость в сечении 1–1 равной нулю (W1 = 0). Применяем уравнение Бернулли к сечению 1 и 2. Сечение 1 и 2 находятся на одном уровне, поэтому Н1 = Н2, следовательно .

без учета (потерь) гидравлического сопротивления отверстия. Скорость потока в сечении 2 , или ,

где φ – коэффициент скорости, учитывающий гидравлическое сопротивление отверстия. Произведение скорости на сечение струи (Fстр) дает объемный расход газа (V). Сечение струи Fстр меньше в ряде случаев сечения отверстия, что учитывают с помощью коэффициента сжатия струи (табл. 2.3): E = Fстр /Fотв.

Если истечение газа происходит через стенку или свод печи, на поду которой поддерживается атмосферное давление, то статическое давление будет обусловлено разностью плотностей . В этом случае .

Источник